Qwen&GPT2 模型架构

GPT2/Qwen2 模型架构

Transformer

在介绍GPT2与Qwen2的模型架构前，首先需要简单的回顾一下Transformer架构，这里就默认读者已经基本了解Transformer了，贴出一个图。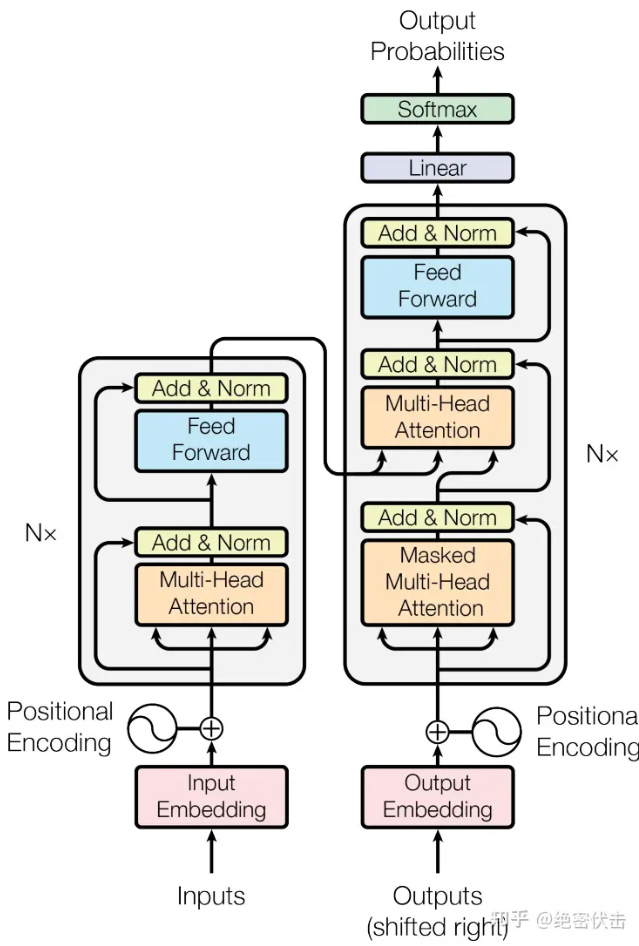

左侧是Encoder部分而右侧是Decoder部分。至于为什么需要将Encoder的输出输入到Decoder当中，以一个机器翻译任务举例。我爱你 -> I love you

首先Encoder的输入为原始的词嵌入，位置编码信息，这部分在另一篇文档中给出了。至于为什么是mask-MultiHead att：在Encoder中我们需要把不同batch(也就是不同的句子集合)都padding为相同的长度，这样适合于向量化运算，所以计算self-att的时候需要把padding的部分mask掉(因为句子这里本身是没有任何消息的)。至于在Bert（Masked Language Modeling - MLM）预训练过程中，他们更类似于做”完形填空”，mask是用来挖空的。

举个例子：我 [masked] 你

经过Encoder的处理之后，输出的矩阵被复制一份，分别经过两个线性层作为Decoder的K与V，作为Decoder中att的输入。

Encoder 输出的同一个矩阵
       |
       +---------------------+
       |                     |
       v                     v
[线性变换 W_k]          [线性变换 W_v]
       |                     |
       v                     v
   第一部分：Key (K)      第二部分：Value (V)
   (用来被 Query 匹配)     (用来被加权提取)
           \             /
            \           /
             \         /
         输入到 Decoder 的 Cross-Attention

其次是Decoder的输入，图中标出了一个Shift-Right，这里是因为Decoder是一个自回归的模型。

通俗的来说 Decoder的预测方式是这样的 [<start>, 预测下一个词] -> [<start>, 单词1, 预测下一个词]，Decoder在预测下一个词的时候需要知道前文。如果直接将原本的词嵌入输入，Decoder是缺失第一个开始标记的(从无到第一个单词的过程)。所以输入的时候Transformer作为有监督的学习，将输入右移就是添加了开始标记[<start>,我, 爱, 你]

另一点是计算注意力分数的时候同样是Masked Att，这里mask是为了保证在训练的时候保证因果性, Decoder属于是预测下一个词，如果提前把下一个词告诉他那么这个预测就没有意义了。

GPT2/GPT3模型结构

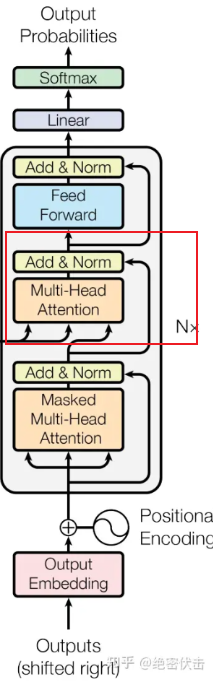
GPT系列使用了Transformer的Decoder架构，他是Decoder-only的模型，相较于原始的transformer，他去掉了中间的Cross-att模块，并经过多次堆叠，大概示例如下:

去掉的Cross-Att模块

[Input]
   |
[Token Emb] + [Positional Emb (可学习的)]
   |
   |--- (堆叠 N 层 Block) ---
   |  [Block i]
   |     |
   |  [Layer Norm]  <-- Pre-Norm
   |     |
   |  [Masked Self-Attention]
   |     |
   |  [Add] (残差连接直接连到 Norm 之前)
   |     |
   |  [Layer Norm]
   |     |
   |  [FFN]
   |     |
   |  [Add]
   |-------------------------
   |
[Layer Norm] (最后的归一化)
   |
[Linear Projection] (映射回词表大小)
   |
[Softmax]

另外他还把归一化提前到了att层前，曾经是post-norm，现在采用了pre-norm。下边是一些模型的参数：
alt text

至于GPT3，他是GPT2堆料的版本，但是采用了新的Sparse-Att技术，因为原有的注意力机制每个单词需要查看他之前所有的单词来获取注意力分数，这个时间复杂度是O(N^2)的，导致显存爆炸。这里的Sparse-Att是有策略地计算注意力分数而不是全局计算。

GPT3还提出了一个概念叫做In-Context-Learning，我认为这和现在的提示词/上下文工程很相似，本质上是因为LLM在训练的过程中有过这样的训练样本，类似与 “问题，答案”这样的。所以在模型中加入一些Context可以有效地提升模型回答的准确率。

Qwen模型架构

Qwen2同样是Transoformer架构，使用了FFN与普通的注意力机制的计算，但是有以下的几个区别：

Group Query Attention
Dual Chunk Attention with yarn
Mixture-Of-Experts (MoE)

和Qwen相同，使用了SwiGLU、RoPE、QKV bias、RMSNorm和pre-norm一系列的trick。

Group Query Attention

在了解GQA前，首先需要看看原始的多头注意力机制(MHA)与多查询注意力机制(MQA)。在MHA计算中，每一个 Query (Q) 头都有自己对应的 Key (K) 头和 Value (V) 头，这样在Inference阶段，显存中需存储所有的Query对应的KV，浪费大量显存。MQA的思想是所有的Q都共享同一组KV头，这样虽然极大的节省了显存，但是对于推理阶段模型的性能也带来了很大损失(因为忽略了大量的KV Cache)。

GQA是一个综合MHA与MQA的一个工程上的权衡，将Q拆分成若干组，一组Q共享同一组KV头，大大减少了KV Cache，同时也保留了MHA多头的特性。

下边是Inference阶段三种注意力机制QKV的对比：

import torch
import torch.nn.functional as F

batch_size = 1
seq_len = 1
d_model = 512
h = 8  # Query heads
d = 64 # Head dimension

# 模拟输入
x = torch.randn(batch_size, seq_len, d_model)
print(x.shape)

# --- 1. MHA (Multi-Head Attention) ---
# 每个 Q 对应一个独立的 K 和 V
# K, V 的头数 = Q 的头数 (8)
Wq_mha = torch.randn(d_model, h * d)
Wk_mha = torch.randn(d_model, h * d)
Wv_mha = torch.randn(d_model, h * d)

q_mha = (x @ Wq_mha).view(batch_size, h, d) # Shape: [1, 8, 64]
k_mha = (x @ Wk_mha).view(batch_size, h, d) # Shape: [1, 8, 64]
v_mha = (x @ Wv_mha).view(batch_size, h, d) # Shape: [1, 8, 64]


# --- 2. MQA (Multi-Query Attention) ---
# 所有 Q 共享同一个 K 和 V
# K, V 的头数 = 1
Wq_mqa = torch.randn(d_model, h * d)
Wk_mqa = torch.randn(d_model, 1 * d)
Wv_mqa = torch.randn(d_model, 1 * d)

q_mqa = (x @ Wq_mqa).view(batch_size, h, d) # Shape: [1, 8, 64]
k_mqa = (x @ Wk_mqa).view(batch_size, 1, d) # Shape: [1, 1, 64]
v_mqa = (x @ Wv_mqa).view(batch_size, 1, d) # Shape: [1, 1, 64]

# 计算时需要将 K, V 广播（Repeat）到 8 个头
k_mqa = k_mqa.expand(-1, h, -1) # [1, 1, 64] -> [1, 8, 64]


# --- 3. GQA (Group Query Attention) ---
# Q 被分成组，每组共享一个 K 和 V
# 假设分成 2 组 (g=2)，每组 4 个 Q 头共享 1 个 KV 头
g = 2
Wq_gqa = torch.randn(d_model, h * d)
Wk_gqa = torch.randn(d_model, g * d)
Wv_gqa = torch.randn(d_model, g * d)

q_gqa = (x @ Wq_gqa).view(batch_size, h, d) # Shape: [1, 8, 64]
k_gqa = (x @ Wk_gqa).view(batch_size, g, d) # Shape: [1, 2, 64]
v_gqa = (x @ Wv_gqa).view(batch_size, g, d) # Shape: [1, 2, 64]

# 计算时需要将 2 个 KV 头“广播”给对应的 Q 组
# 这里的 repeat_interleave 表示每个 KV 头复制 4 次 (8/2=4)
k_gqa = k_gqa.repeat_interleave(h // g, dim=1) # [1, 2, 64] -> [1, 8, 64]

对比MHA与GQA，如果Group=8，那么模型在推理阶段就可以获得更快的上下文长度，32k -> 32k*8或者是一张单独的显卡可以服务更多的用户。

Dual Chunk Attention with Yarn

Dual Chunk Attention

Dual Chunk Attention (DCA) 与 YaRN (Yet another RoPE extensioN) 是两种为了解决 Transformer “长文本瓶颈” 而产生的互补技术。

DCA 的核心思想是将超长的序列切分成多个 Chunk（块），并利用分块矩阵的特性来降低计算复杂度和显存占用。在处理长达 100k 甚至 1M 的文本时，全量注意力矩阵（Attention Matrix）是 $N^2$ 级别的，显存根本装不下。DCA 通过以下两个维度进行分解：

Intra-Chunk Attention（块内注意力）：在每个局部的小块内部进行精细的注意力计算（捕捉局部特征）。
Inter-Chunk Attention（块间注意力）：块与块之间通过压缩或特定的聚合方式进行信息交换（捕捉长距离依赖）。

这种情况下就不需要维护一个 $N^2$ 的矩阵，在读取时就不需要一次性将所有的注意力机制全部读入显存进行注意力计算。假设当前有1M的KV Cache，当Inference阶段(利用MHA)预测下一个词的时候，当前的Q需要与1M的KV进行计算。

1M上下文需要的计算量估计：
Context Length = 1M, head_dimension = 128, h_num = 64
第一步计算Q(维度为1*128) K(1M *128)的乘积,一个head计算量为 2 * Context Length * head_dimension（乘加各一次）
64个注意力头需要计算 2 * Context Length * head_dimension * h_num
第二步计算与 V(1M * 128) 的乘积
总计算量大致为 $\mathbf{16.38}$ G FLOPs，两个计算量相加约等于 32G FLOPs。
上面只是计算开销，真正耗时的部分是从显存中搬运KV矩阵，由于上下文长度巨大，导致在计算的时候内存局部性降低

DCA 的加速方式：它将 $N$ 划分为一个个固定大小的 Chunk。

计算块内（Intra-Chunk）时：它只需要加载当前所属块的 KV Cache。这部分数据量小，可以完全放入 GPU 极速的 SRAM（Shared Memory）中反复使用，大大减少了对慢速显存的访问次数。
计算块间（Inter-Chunk）时：它通过一种“高度压缩”或者“层级化”的索引来读取其他块。比如只读其他块的代表性特征（Centroids），而不是读所有原始 KV。读的数据量少了，速度自然就快了。

从而实现了显存上的“分治”。

YaRN (Yet another RoPE extensioN)

YaRN是对RoPE的一种外推，在RoPE中，位置会被两两分组，第m个位置的token都被添加了一个旋转角度 $m\theta$。RoPE相较于Transformer的位置编码的好处，参考RoPE位置编码那一篇blog。RoPE本身对于长度外推的方式是线性缩放，如果一个模型本身的上下文长度是4k的，那么RoPE位置编码的频率范围就应该是 $[0,4000 \theta]$,如果给这个模型传入了1M大小的上下文，那么此时的RoPE的频率范围理应是 $[0, 1000000\theta]$，但是模型本身不支持这个大小，所以对这个范围进行一个频率的缩放，将旋转的角度除以一个比例(例如$s = 1000000 / 4000$)，这样虽然实现了位置的外推，但是两两分组的单词频率的差异也变小了，导致模型识别不同的位置出现问题。

YaRN的思想是分频外推，既然线性缩放的方式会损失高频细节，那么不如将高频、中频、低频分离进行缩放处理，从而实现上下文长度的外推。
在 RoPE 中，每个维度 $i$ 都有一个特定的旋转频率 $\theta_i$，对应的波长 $\lambda_i$ 定义为：
$$\lambda_i = \frac{2\pi}{\theta_i} = 2\pi \cdot 10000^{2i/d}$$

1. 高频维度

对应维度：维度索引 $i$ 较小的部分。
数学特征：频率 $\theta_i$ 很大，波长 $\lambda_i$ 很短。
在YaRN中的角色：由于波长远小于原始预训练长度（如 $L_{old}=2048$），这些维度在训练时已经“见过”成百上千次的完整旋转周期。模型对这些旋转非常敏感且熟悉。YaRN 认为这些维度不应该被插值（缩放），否则会模糊模型对相邻词汇的精确感知。

2. 低频维度

对应维度：维度索引 $i$ 较大的部分。
数学特征：频率 $\theta_i$ 极小，波长 $\lambda_i$ 极大。
在YaRN中的角色：当序列长度扩展到 128k 时，这些维度的旋转角度会超出训练时的范围。YaRN 对这些维度进行完全线性插值。因为它们旋转得慢，稍微缩放一下频率，模型依然能理解这种缓慢的变化，从而感知到极远距离的 Token。

3. 中频维度

对应维度：维度索引 $i$ 处于中间(训练时模型上下文长度)的部分。
在YaRN中的角色：YaRN 使用一个平滑函数 $a(i)$，让这部分维度的缩放比例从1缓慢过渡到 $s$（扩展倍数）。

插值函数

YaRN 引入一个插值函数 $a(i)$，修正后的频率 $\theta’_i$ 为：

$$\theta’_i = \frac{\theta_i}{\gamma_i}$$

其中缩放系数 $\gamma_i$ 的计算如下：

$$\gamma_i = (1 - a(i)) \cdot 1 + a(i) \cdot s$$

而 $a(i)$ 是根据维度索引 $i$ 确定的平滑函数：

$$a(i) = \text{clamp}\left( \frac{i - r_{min}}{r_{max} - r_{min}}, 0, 1 \right)$$

其中 $r_{min}$ 和 $r_{max}$ 是由超参数 $\alpha, \beta$ 导出的维度边界。

我们将位置编码进行插值（即减小频率）时，在计算点积注意力 $QK^T$ 时，平均距离上的余弦相似度会变大。这会导致 Softmax 后的分布变得更加平滑（熵增加），模型会丧失对特定 Token 的关注能力。YaRN 通过修改温度系数来补偿这种损失。在计算 Attention Score 时，引入修正因子 $\sqrt{\hat{s}}$：

$$\text{Attention}(Q, K, V) = \text{softmax}\left( \frac{QK^T \cdot \sqrt{\hat{s}}}{\sqrt{d_k}} \right)V$$

其中 $\hat{s}$ 的经验公式通常与 $s$ 有关。在 YaRN 的实现中，通过实验拟合了一个关于 $s$ 的缩放因子 $m(s)$，用于缩放 $Q$ 和 $K$ 的点积：

$$m(s) = 0.1 \cdot \ln(s) + 1.0$$

修正后的计算通常直接作用于权重：

$$Score = \frac{QK^T}{\sqrt{d_k}} \cdot m(s)$$

MoE

MoE(混合专家模型)，采用了一种根据问题分治的策略，有一点像网络中的“路由”的概念。

MoE的核心组件

在传统的Transformer中，每一个Block都只有一个FFN，在MoE中，一个Block有多个这样的FFN，每一份就是一个专家。

专家层
每个Block中的各个专家是相互独立的，拥有自身独立的权重矩阵，但是他们的结构相同；同时由于专家之间相互独立，GPU可以让不同的专家处理不同的Token。
门控网络
门控网络本质上是一个分类器，对于输入的token向量 $x$，Router计算对应的分数 $Score = x \cdot W_g$，Softmax处理之后得到各个专家的概率分布，最后inference阶段选取概率最高的Tok-K个专家。

补充： MoE中除了处理各个领域知识的专家，同时还有一个共享专家(shared expert),这个共享专家不参与Router的竞争。

综合上面的这些，就能理解Qwen2的总参数量虽然很大，但是实际推理的时候只有一部分的专家被激活了。

#Transformer

Qwen&GPT2 模型架构

http://example.com/2026/01/19/Qwen-GPT2-architecture/

作者

Soya

发布于

2026年1月19日

许可协议

completable-future学习笔记上一篇

CUDA实现并行求和下一篇